- Slēgtai ķēdei
- Atsevišķa sekcija un pilnīga elektriskā ķēde
- Elektriskās ķēdes strāvas posma aprēķins
- Aprēķinu iespēja visai ķēdei
- Likuma ietekme uz mainīgo
- EML avots pilnā ķēdē
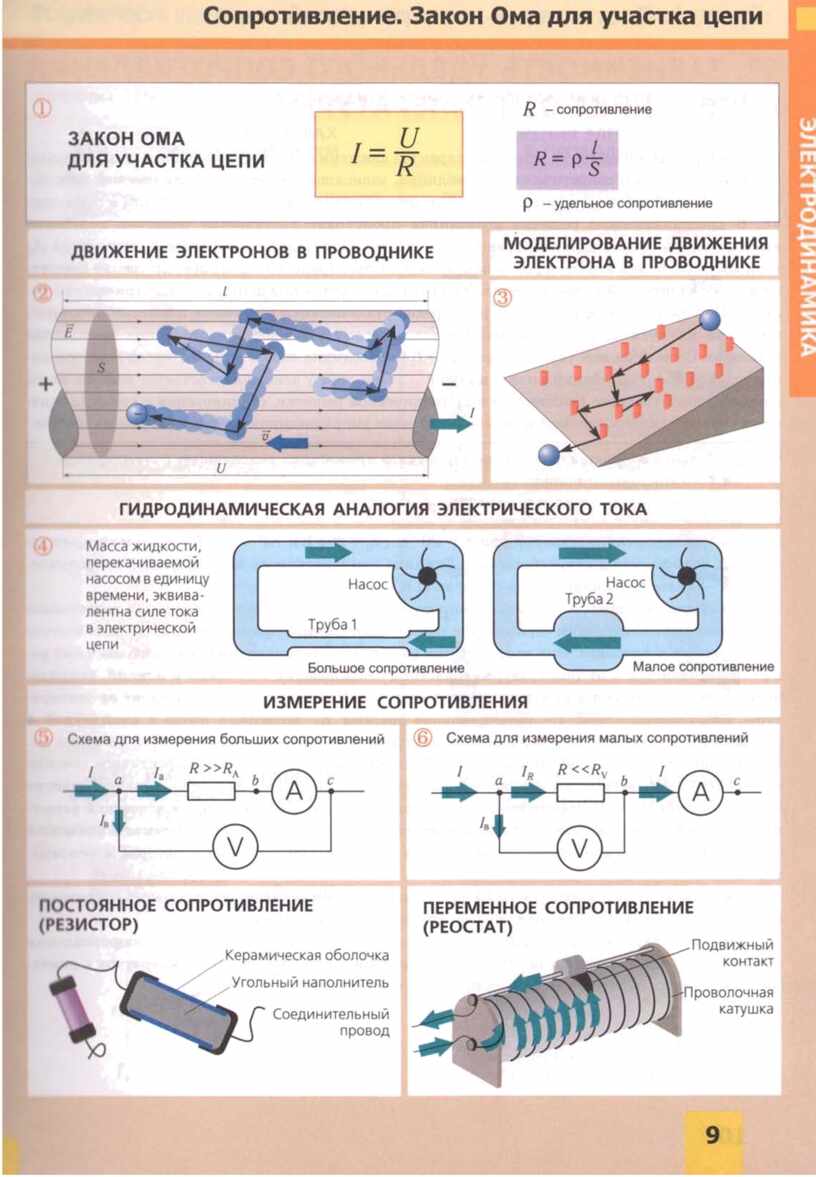
- R - elektriskā pretestība
- Nevienmērīga līdzstrāvas ķēdes sadaļa
- Elementu sērijveida un paralēlais savienojums
- Virknē savienotu pretestības elementu ķēde
- Paralēli savienotu pretestības elementu ķēde
- Likuma integrālās un diferenciālās formas
- Izpratne par strāvu un pretestību
- Oma likums maiņstrāvai
- Kad notiek Oma likums
- Kirhhofa likumi.
- Pamatjēdzieni
- Spēks un spriedze
- Vadītāja pretestība
- Oma likuma interpretācija
- Paralēlais un seriālais savienojums
- seriālais savienojums
- Paralēlais savienojums
- Kas mums nodrošina paralēlo un seriālo savienojumu?
- Ideāls EMF avots
- Diferenciālā formā
Slēgtai ķēdei
Slēgta ķēde nozīmē slēgtu elektrisko savienojumu, caur kuru cirkulē strāva. Kad ir virkne vadu, kas savienojas viens ar otru un pabeidz ķēdi tā, ka es virzos no viena apļa gala līdz otram, tā būs slēgta ķēde.
EMF (E) - apzīmē un mēra voltos un attiecas uz spriegumu, ko rada akumulators vai magnētiskais spēks saskaņā ar Faradeja likumu, kas nosaka, ka laikā mainīgs magnētiskais lauks inducēs elektrisko strāvu.
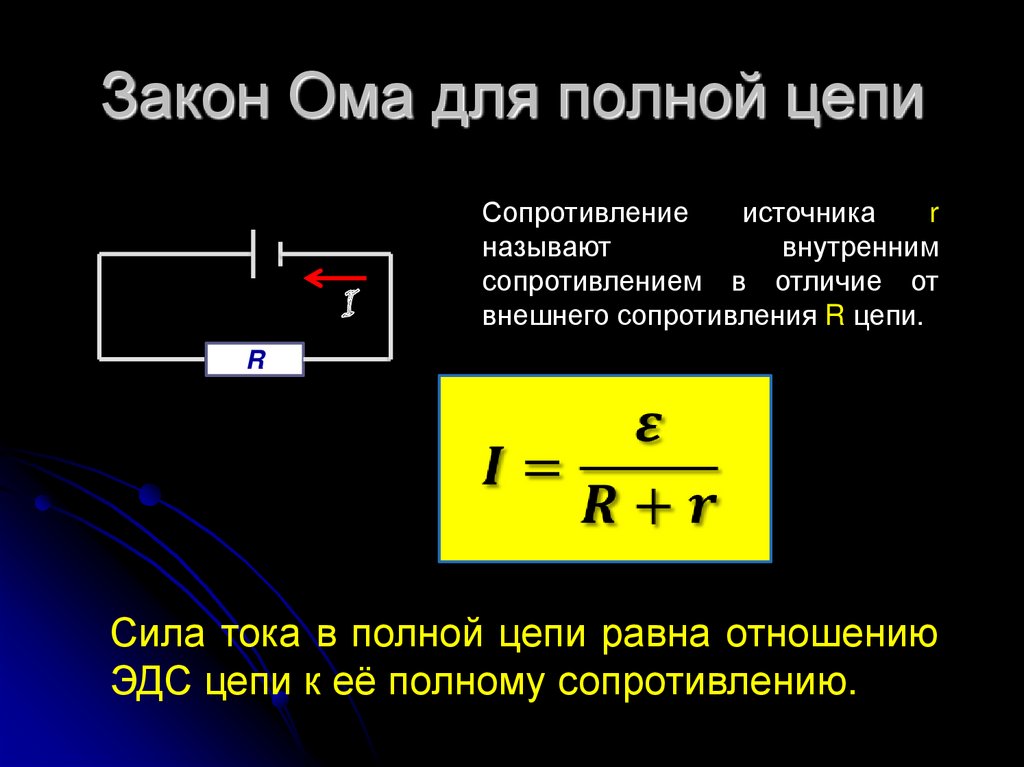
Tad: E = IR + Ir
E \u003d I (R + r)
I \u003d E / (R + r)
Kur: r ir strāvas avota pretestība.
Šī izteiksme ir pazīstama kā Ohma likums par slēgtās cilpas ķēdēm.
Heterogēna ķēde
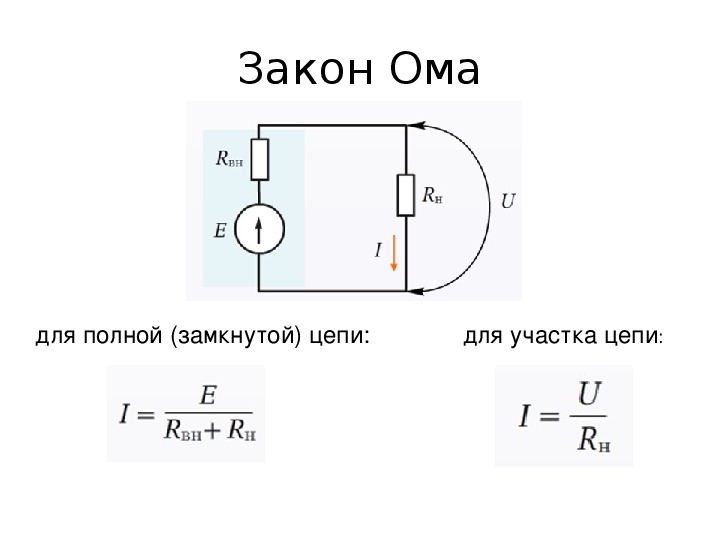
Atsevišķa sekcija un pilnīga elektriskā ķēde
Oma likumu, kas piemērots sekcijai vai visai ķēdei, var aplūkot divās aprēķina opcijās:
- Atsevišķa īsa sadaļa. Tā ir daļa no ķēdes bez EML avota.
- Pilna ķēde, kas sastāv no vienas vai vairākām sekcijām. Tas ietver arī EML avotu ar savu iekšējo pretestību.
Elektriskās ķēdes strāvas posma aprēķins
Šajā gadījumā tiek piemērota pamatformula I \u003d U / R, kurā I ir strāvas stiprums, U ir spriegums, R ir pretestība. Saskaņā ar to var formulēt vispārpieņemtu Ohma likuma interpretāciju:
Šis formulējums ir pamats daudzām citām formulām, kas tiek piedāvātas uz tā saukto "kumelīšu" grafiskajā dizainā. Sektorā P - tiek noteikta jauda, I, U un R sektoros - tiek veiktas darbības, kas saistītas ar strāvas stiprumu, spriegumu un pretestību.
Katra izteiksme - gan pamata, gan papildu, ļauj aprēķināt precīzus elementu parametrus, kas paredzēti izmantošanai ķēdē.
Speciālisti, kas strādā ar elektriskajām ķēdēm, veic ātru jebkura parametra noteikšanu, izmantojot attēlā parādīto trīsstūra metodi.
Aprēķinos jāņem vērā vadu pretestība, kas savieno sekcijas elementus. Tā kā tie ir izgatavoti no dažādiem materiāliem, šis parametrs katrā gadījumā būs atšķirīgs.Ja nepieciešams veidot pilnu ķēdi, tad galveno formulu papildina ar sprieguma avota, piemēram, akumulatora, parametriem.
Aprēķinu iespēja visai ķēdei
Pilna ķēde sastāv no atsevišķām sekcijām, kas apvienotas vienā veselumā kopā ar sprieguma avotu (EMF). Tādējādi esošo sekciju pretestību papildina pieslēgtā avota iekšējā pretestība. Tāpēc galvenā interpretācija, kas tika apspriesta iepriekš, skanēs šādi: I = U / (R + r). Šeit jau ir pievienots EML avota pretestības indikators (r).
No tīrās fizikas viedokļa šis rādītājs tiek uzskatīts par ļoti mazu vērtību. Tomēr praksē, aprēķinot sarežģītas shēmas un shēmas, speciālisti ir spiesti to ņemt vērā, jo papildu pretestība ietekmē darba precizitāti. Turklāt katra avota struktūra ir ļoti neviendabīga, kā rezultātā pretestību dažos gadījumos var izteikt ar diezgan augstiem rādītājiem.
Iepriekš minētie aprēķini tiek veikti saistībā ar līdzstrāvas ķēdēm. Darbības un aprēķini ar maiņstrāvu tiek veikti saskaņā ar citu shēmu.
Likuma ietekme uz mainīgo
Ar maiņstrāvu ķēdes pretestība būs tā sauktā pretestība, kas sastāv no aktīvās pretestības un reaktīvās pretestības slodzes. Tas ir saistīts ar elementu klātbūtni ar induktīvām īpašībām un sinusoidālu strāvas vērtību. Spriegums ir arī mainīgs lielums, kas darbojas saskaņā ar tā pārslēgšanas likumiem.
Tāpēc Ohma likuma maiņstrāvas ķēdes dizains tiek aprēķināts, ņemot vērā specifiskos efektus: strāvas lieluma novadīšanu vai atpalikšanu no sprieguma, kā arī aktīvās un reaktīvās jaudas klātbūtni.Savukārt pretestība ietver induktīvos vai kapacitatīvos komponentus.
Visas šīs parādības atbildīs formulai Z \u003d U / I vai Z \u003d R + J * (XL - XC), kurā Z ir pretestība; R - aktīvā slodze; XL, XC - induktīvās un kapacitatīvās slodzes; J ir korekcijas koeficients.
EML avots pilnā ķēdē
Lai slēgtā ķēdē notiktu elektriskā strāva, šajā ķēdē jābūt vismaz vienam īpašam elementam, kurā notiks lādiņu pārnešana starp tās poliem. Spēki, kas nes lādiņus šī elementa iekšpusē, to dara pret elektrisko lauku, kas nozīmē, ka to būtībai ir jāatšķiras no elektriskajiem. Tāpēc šādus spēkus sauc par trešām personām.
Rīsi. 1. Ārējie spēki fizikā.
Elektriskās ķēdes elementu, kurā darbojas ārējie spēki, lai pārnestu lādiņus pret elektriskā lauka darbību, sauc par strāvas avotu. Tās galvenā īpašība ir ārējo spēku lielums. Lai to raksturotu, tiek ieviests īpašs mērs - Elektromotīvs spēks (EMF), to apzīmē ar burtu $\mathscr{E}$.
Strāvas avota EMF vērtība ir vienāda ar ārējo spēku attiecību lādiņa pārnešanai pret šī lādiņa vērtību:
$$\mathscr{E}={A_{st}\vairāk nekā q}$$
Tā kā EML nozīme ir ļoti tuva elektriskā sprieguma nozīmei (atgādināt, spriegums ir lādiņu nesošā elektriskā lauka veiktā darba attiecība pret šī lādiņa vērtību), tad EMF, tāpat kā spriegumu, mēra Volti:
$$1B={J\overCl}$$
Otrs svarīgākais reāla strāvas avota elektriskais raksturlielums ir tā iekšējā pretestība.Kad lādiņi tiek pārnesti starp spailēm, tie mijiedarbojas ar EML avota vielu, un tāpēc elektriskās strāvas avots arī rada zināmu pretestību. Iekšējā pretestība, tāpat kā parastā pretestība, tiek mērīta omos, bet to apzīmē ar mazo latīņu burtu $r$.

Rīsi. 2. Strāvas avotu piemēri.
R - elektriskā pretestība
Pretestība ir sprieguma apgrieztā vērtība, un to var salīdzināt ar ķermeņa pārvietošanas efektu pret kustību tekošā ūdenī. R vienība ir Om, ko apzīmē ar lielo grieķu burtu Omega.
Pretestības apgrieztā vērtība (1/R) ir pazīstama kā vadītspēja, kas mēra objekta spēju vadīt lādiņu, izteiktu Siemens vienībās.
Izmantoto ģeometriski neatkarīgo lielumu sauc par pretestību un parasti apzīmē ar grieķu simbolu r.
Papildus informācija. Oma likums palīdz noteikt trīs svarīgus elektrotīkla darbības rādītājus, kas vienkāršo jaudas aprēķinu. Tas nav piemērojams vienpusējiem tīkliem ar tādiem elementiem kā diode, tranzistors un tamlīdzīgi. Un arī tas nav attiecināms uz nelineāriem elementiem, kuru piemēri ir tiristori, jo šo elementu pretestības vērtība mainās ar dažādu spriegumu un strāvu.
Augstākās frekvencēs izplatītā uzvedība kļūst dominējoša. Tas pats notiek ar ļoti garām elektropārvades līnijām. Pat tik zemā frekvencē kā 60 Hz ļoti garai pārvades līnijai, piemēram, 30 km, ir sadalīts raksturs. Galvenais iemesls ir tas, ka efektīvie elektriskie signāli, kas izplatās ķēdēs, ir elektromagnētiskie viļņi, nevis volti un ampēri, kurus inficē elektromagnētiskais vilnis.Vadītāji vienkārši darbojas kā viļņu vadotnes. Tātad, piemēram, koaksiālais kabelis parādīs Z = 75 omi, pat ja tā līdzstrāvas pretestība ir niecīga.
Oma likums ir elektrotehnikas pamatlikums. Tam ir daudz praktisku pielietojumu visās elektriskās ķēdēs un elektroniskajos komponentos.
Visizplatītākie Ohma likuma piemērošanas piemēri:
- Elektriskajam sildītājam piegādātā jauda. Ņemot vērā sildītāja spoles pretestību un pielietoto spriegumu, var aprēķināt šim sildītājam piegādāto jaudu.
- Drošinātāju izvēle. Tie ir aizsardzības komponenti, kas ir virknē savienoti ar elektroniskām ierīcēm. Drošinātāji/CB ir nomināli ampēros. Pašreizējais drošinātāja nomināls tiek aprēķināts, izmantojot Ohma likumu.
- Elektronisko ierīču projektēšana. Elektroniskām ierīcēm, piemēram, klēpjdatoriem un mobilajiem tālruņiem, ir nepieciešams līdzstrāvas barošanas avots ar noteiktu strāvas vērtību. Tipiskām mobilo tālruņu baterijām ir nepieciešams 0,7-1 A. Lai kontrolētu strāvas ātrumu, kas plūst caur šiem komponentiem, tiek izmantots rezistors. Oma likumu izmanto, lai aprēķinātu nominālo strāvu tipiskā ķēdē.
Savulaik Oma secinājumi kļuva par katalizatoru jauniem pētījumiem elektroenerģijas jomā, un šodien tie nav zaudējuši savu nozīmi, jo uz tiem balstās mūsdienu elektrotehnika. 1841. gadā Omam tika piešķirts Karaliskās biedrības augstākais apbalvojums - Koplija medaļa, un termins "Om" tika atzīts par pretestības vienību jau 1872. gadā.
Nevienmērīga līdzstrāvas ķēdes sadaļa
Neviendabīgai struktūrai ir tāda ķēdes sadaļa, kurā papildus vadītājiem un elementiem ir strāvas avots. Aprēķinot kopējo strāvas stiprumu šajā jomā, jāņem vērā tā EMF.
Pastāv formula, kas definē neviendabīgas vietas galvenos parametrus un procesus: q = q0 x n x V. Tās rādītājus raksturo šādi:
- Lādiņu kustības procesā (q) tie iegūst noteiktu blīvumu. Tās veiktspēja ir atkarīga no strāvas stipruma un vadītāja šķērsgriezuma laukuma (S).
- Noteiktas koncentrācijas (n) apstākļos ir iespējams precīzi norādīt vienā laika periodā pārvietoto vienības lādiņu skaitu (q0).
- Aprēķiniem vadītājs nosacīti tiek uzskatīts par cilindrisku sekciju ar noteiktu tilpumu (V).
Savienojot vadītāju ar akumulatoru, tas pēc kāda laika izlādēsies. Tas ir, elektronu kustība pakāpeniski palēninās un galu galā apstājas pavisam. To veicina vadītāja molekulārais režģis, kas neitralizē elektronu sadursmi savā starpā un citus faktorus. Lai pārvarētu šādu pretestību, papildus jāpieliek noteikti trešo pušu spēki.
Aprēķinu laikā šie spēki tiek pieskaitīti Kulona spēkiem. Turklāt, lai pārsūtītu vienības lādiņu q no 1. punkta uz 2., būs jāveic darbs A1-2 vai vienkārši A12. Šim nolūkam tiek izveidota potenciālu starpība (ϕ1 - ϕ2). Līdzstrāvas avota iedarbībā rodas EML, kas pārvieto lādiņus pa ķēdi. Kopējā sprieguma lielumu veidos visi iepriekš minētie spēki.
Aprēķinos ir jāņem vērā pieslēguma polaritāte līdzstrāvas padevei. Mainot spailes, mainīsies arī EMF, paātrinot vai palēninot lādiņu kustību.
Elementu sērijveida un paralēlais savienojums
Elektriskās ķēdes elementiem (ķēdes posmam) raksturīgs moments ir virknes vai paralēlais savienojums.
Attiecīgi katram savienojuma veidam ir pievienots atšķirīgs strāvas plūsmas un sprieguma padeves raksturs. Šajā sakarā Ohma likums tiek piemērots arī dažādos veidos atkarībā no elementu iekļaušanas iespējas.
Virknē savienotu pretestības elementu ķēde
Attiecībā uz virknes savienojumu (ķēdes posms ar diviem komponentiem) tiek izmantots formulējums:
- es = es1 = es2 ;
- U = U1 + U2 ;
- R=R1 + R2
Šis formulējums skaidri parāda, ka neatkarīgi no virknē savienoto pretestības komponentu skaita strāva, kas plūst ķēdes posmā, nemaina vērtību.
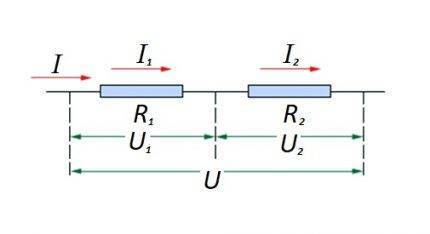 Pretestības elementu savienošana ķēdes daļā virknē viens ar otru. Šai opcijai ir savs aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U, U1, U2 - pielietotais spriegums
Pretestības elementu savienošana ķēdes daļā virknē viens ar otru. Šai opcijai ir savs aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U, U1, U2 - pielietotais spriegums
Sprieguma daudzums, kas tiek pievadīts ķēdes aktīvajiem pretestības komponentiem, ir summa, kas tiek pievienota EML avota vērtībai.
Šajā gadījumā katra atsevišķa komponenta spriegums ir: Ux = I * Rx.
Kopējā pretestība jāuzskata par visu ķēdes pretestības komponentu vērtību summu.
Paralēli savienotu pretestības elementu ķēde
Gadījumā, ja ir paralēls pretestības komponentu savienojums, formulējums tiek uzskatīts par taisnīgu attiecībā uz vācu fiziķa Oma likumu:
- es = es1 + es2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1/R2 + …
Ja tiek izmantoti paralēlie un seriālie savienojumi, nav izslēgtas “jaukta” tipa ķēžu sekciju kompilēšanas iespējas.
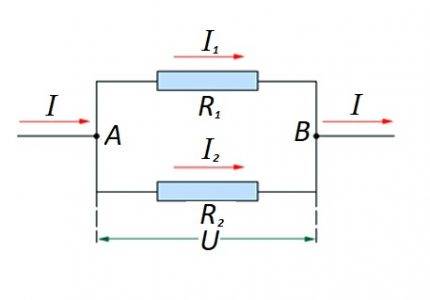 Pretestības elementu savienojums ķēdes daļā paralēli viens otram. Šim variantam tiek piemērots savs aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U - pielietotais spriegums; A, B - ieejas / izejas punkti
Pretestības elementu savienojums ķēdes daļā paralēli viens otram. Šim variantam tiek piemērots savs aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U - pielietotais spriegums; A, B - ieejas / izejas punkti
Šādām opcijām aprēķinu parasti veic, sākotnēji aprēķinot paralēlā savienojuma pretestību. Tad rezistora vērtība tiek pievienota sērijveidā.
Likuma integrālās un diferenciālās formas
Visi iepriekš minētie punkti ar aprēķiniem ir piemērojami apstākļiem, kad, tā sakot, "viendabīgas" struktūras vadītāji tiek izmantoti kā daļa no elektriskajām ķēdēm.
Tikmēr praksē nereti nākas saskarties ar shēmas uzbūvi, kur dažādās jomās mainās vadītāju struktūra. Piemēram, tiek izmantoti lielāka šķērsgriezuma vadi vai, gluži pretēji, mazāki, kas izgatavoti uz dažādu materiālu bāzes.
Lai ņemtu vērā šādas atšķirības, pastāv tā sauktā "diferenciālintegrāļa Ohma likuma" variācija. Bezgalīgi mazam vadītājam strāvas blīvuma līmeni aprēķina atkarībā no intensitātes un vadītspējas vērtības.
Saskaņā ar diferenciālo aprēķinu tiek ņemta formula: J = ό * E
Attiecīgi integrāļa aprēķinam formulējums: I * R = φ1 - φ2 + έ
Tomēr šie piemēri ir drīzāk tuvāki augstākās matemātikas skolai un netiek faktiski izmantoti vienkārša elektriķa praksē.
Izpratne par strāvu un pretestību
Sāksim ar elektriskās strāvas jēdzienu. Īsāk sakot, elektriskā strāva attiecībā pret metāliem ir elektronu virzīta kustība - negatīvi lādētas daļiņas. Tie parasti tiek attēloti kā mazi apļi.Mierīgā stāvoklī viņi pārvietojas nejauši, pastāvīgi mainot virzienu. Noteiktos apstākļos - potenciālās starpības parādīšanās - šīs daļiņas sāk noteiktu kustību kādā virzienā. Šī kustība ir elektriskā strāva.
Lai padarītu to skaidrāku, mēs varam salīdzināt elektronus ar ūdeni, kas izlijis kādā plaknē. Kamēr lidmašīna stāv, ūdens nekustas. Bet, tiklīdz parādījās slīpums (parādījās potenciāla atšķirība), ūdens sāka kustēties. Tas pats ir ar elektroniem.
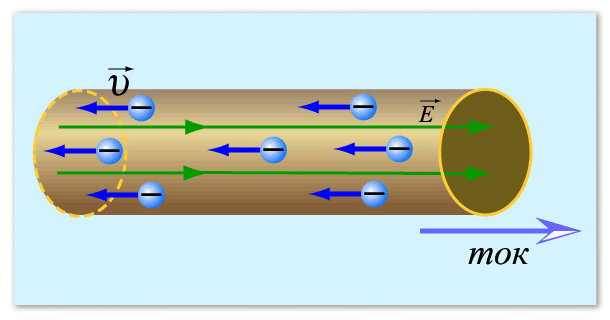
Šādi var iedomāties elektrisko strāvu
Tagad mums ir jāsaprot, kas ir pretestība un kāpēc viņiem ir atgriezeniskā saite ar strāvas stiprumu: jo lielāka pretestība, jo mazāka strāva. Kā jūs zināt, elektroni pārvietojas pa vadītāju. Parasti tie ir metāla stieples, jo metāliem ir laba spēja vadīt elektrību. Mēs zinām, ka metālam ir blīvs kristāliskais režģis: daudzas daļiņas, kas ir ciešas un savstarpēji saistītas. Elektroni, veidojot ceļu starp metāla atomiem, saduras ar tiem, kas apgrūtina to kustību. Tas palīdz ilustrēt vadītāja pretestību. Tagad kļūst skaidrs, kāpēc jo lielāka pretestība, jo mazāks strāvas stiprums – jo vairāk daļiņu, jo grūtāk elektroniem pārvarēt ceļu, viņi to dara lēnāk. Šķiet, ka tas ir atrisināts.
Ja jums ir vēlme šo atkarību pārbaudīt empīriski, atrodiet mainīgo rezistoru, pievienojiet virknē rezistoru - ampērmetru - strāvas avotu (akumulatoru). Vēlams ķēdē ievietot arī slēdzi - parastu pārslēgšanas slēdzi.
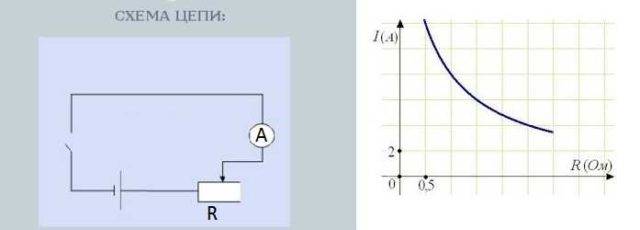
Shēma strāvas atkarības no pretestības pārbaudei
Pagriežot rezistora pogu, tiek mainīta pretestība.Tajā pašā laikā mainās arī ampērmetra rādījumi, kas mēra strāvas stiprumu. Turklāt, jo lielāka pretestība, jo mazāk bultiņa novirzās - jo mazāka strāva. Jo mazāka pretestība, jo vairāk bultiņa novirzās - strāva ir lielāka.
Strāvas atkarība no pretestības ir gandrīz lineāra, tas ir, grafikā tā tiek atspoguļota kā gandrīz taisna līnija. Kāpēc gandrīz - par to būtu jārunā atsevišķi, bet tas jau ir cits stāsts.
Oma likums maiņstrāvai
Aprēķinot maiņstrāvas ķēdes, pretestības jēdziena vietā tiek ieviests jēdziens "pretestība". Pretestība tiek apzīmēta ar burtu Z, tā ietver slodzes R aktīvo pretestībua un pretestība X (vai Rr). Tas ir saistīts ar sinusoidālās strāvas (un jebkura cita veida strāvu) formu un induktīvo elementu parametriem, kā arī pārslēgšanas likumiem:
- Strāva induktīvā ķēdē nevar mainīties uzreiz.
- Spriegums ķēdē ar kapacitāti nevar mainīties uzreiz.
Tādējādi strāva sāk aizkavēties vai vadīt spriegumu, un šķietamā jauda tiek sadalīta aktīvajā un reaktīvajā.
U=I/Z
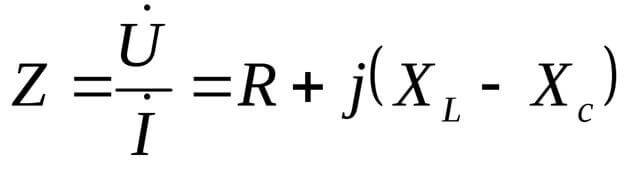
XL un XC ir slodzes reaktīvās sastāvdaļas.
Šajā sakarā tiek ieviesta vērtība cosФ:
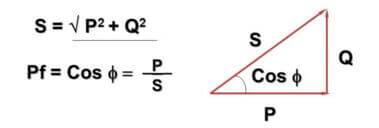
Šeit - Q - reaktīvā jauda maiņstrāvas un induktīvi-kapacitatīvo komponentu dēļ, P - aktīvā jauda (izkliedēta aktīvajos komponentos), S - šķietamā jauda, cosФ - jaudas koeficients.
Jūs, iespējams, pamanījāt, ka formula un tās attēlojums krustojas ar Pitagora teorēmu. Tas ir taisnība, un leņķis Ф ir atkarīgs no tā, cik liela ir slodzes reaktīvā sastāvdaļa - jo lielāka tā ir, jo lielāka. Praksē tas noved pie tā, ka tīklā faktiski plūstošā strāva ir lielāka par to, ko ņem vērā sadzīves skaitītājs, savukārt uzņēmumi maksā par pilnu jaudu.
Šajā gadījumā pretestība tiek parādīta sarežģītā formā:
Šeit j ir iedomāta vienība, kas raksturīga vienādojumu sarežģītajai formai. Retāk saukts par i, bet elektrotehnikā tiek apzīmēta arī maiņstrāvas efektīvā vērtība, tāpēc, lai neapjuktu, labāk izmantot j.
Iedomātā vienība ir √-1. Loģiski, ka kvadrātā nav tāda skaitļa, kas var beigties ar negatīvu rezultātu "-1".
Kad notiek Oma likums
Radīt ideālus apstākļus nav viegli. Pat tīros vadītājos elektriskā pretestība mainās atkarībā no temperatūras. Tā samazināšanās samazina kristāla režģa molekulu aktivitāti, kas atvieglo brīvo lādiņu kustību. Noteiktā "sasalšanas" līmenī rodas supravadītspējas efekts. Karsējot tiek novērots pretējs efekts (vadītspējas pasliktināšanās).
Tajā pašā laikā elektrolīti, metāli un daži keramikas veidi saglabā elektrisko pretestību neatkarīgi no strāvas blīvuma. Parametru stabilitāte, saglabājot noteiktu temperatūras režīmu, ļauj pielietot Ohma likuma formulas bez papildu korekcijām.
Pusvadītāju materiāliem un gāzēm ir raksturīga dažāda elektriskā pretestība. Šo parametru būtiski ietekmē strāvas intensitāte vadības skaļumā. Lai aprēķinātu veiktspējas raksturlielumus, jāizmanto specializētas aprēķina metodes.
Ja tiek ņemta vērā maiņstrāva, aprēķina metode tiek koriģēta. Šajā gadījumā būs jāņem vērā reaktīvo komponentu klātbūtne. Ar pretestības pretestības raksturu ir iespējams pielietot aplūkotās aprēķinu tehnoloģijas, pamatojoties uz Ohma likuma formulām.
Kirhhofa likumi.
Izplatīšana
strāvas elektriskās ķēdes atzaros
ievēro pirmo Kirhhofa likumu,
un spriegumu sadalījums pa sekcijām
ķēde pakļaujas otrajam Kirhhofa likumam.
Kirhofa likumi
kopā ar Oma likumu ir galvenie
elektrisko ķēžu teorijā.
Pirmais
Kirhhofa likums:
Algebriskā
strāvu summa mezglā ir nulle:
i
= 0 (19)
Kur
i
ir zaru skaits, kas saplūst noteiktā mezglā.
Tas ir, summēšana
sniedzas līdz strāvām zaros,
kas saplūst aplūkotajā
mezgls.
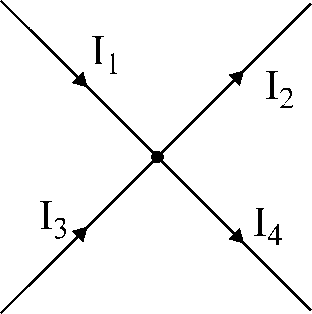
17. att. Ilustrācija
uz Kirhhofa pirmo likumu.
Numurs
vienādojumi, kas sastādīti saskaņā ar pirmo
Kirhhofa likumu nosaka pēc formulas:
Nup
= Nu
– 1,
Kur
Nu
ir mezglu skaits aplūkotajā ķēdē.
Strāvas pazīmes iekšā
vienādojumi tiek ņemti vērā, ņemot vērā atlasīto
pozitīvs virziens. Zīmes plkst
strāvas ir vienādas, ja strāvas ir vienādas
orientēts uz to
mezgls.
Piemēram,
17. attēlā redzamajam mezglam:
mēs piešķiram zīmes strāvām, kas plūst uz mezglu
"+", un uz strāvām, kas plūst no mezgla - zīmes
«-».
Tad vienādojums
saskaņā ar pirmo Kirhhofa likumu tas tiks uzrakstīts
Tātad:
es1
– es2
+ es3
– es4
= 0.
vienādojumi,
sastādīts saskaņā ar pirmo Kirhhofa likumu,
tiek saukti par mezgliem.
Šis
likums pauž to, ka mezglā
elektriskais lādiņš neuzkrājas
un netiek patērēts. Elektrības daudzums
maksa, kas nāk uz vietni, ir vienāda ar summu
maksas atstājot mezglu vienā un tajā pašā
tas pats laika sprīdis.
Otrkārt
Kirhhofa likums:
Algebriskā
emf summa jebkurā slēgtā ķēdē
ķēde ir vienāda ar kritienu algebrisko summu
spriegums uz šīs ķēdes elementiem:
Ui
=
Ei
IiRi=Ei(20)
Kur
i
- elementa numurs (pretestība vai
sprieguma avots) aplūkotajā
kontūru.
**Numurs
vienādojumi, kas sastādīti saskaņā ar otro
Kirhhofa likumu nosaka pēc formulas:
Nup
= Nb
- Nu
+ 1 – Ned.s.
Kur
Nb
- elektriskās ķēdes zaru skaits;
Nu
— mezglu skaits;
Ned.s.
ir ideālo emf avotu skaits.
18. att. Ilustrācija
uz Kirhhofa otro likumu.
Priekš,
pareizi uzrakstīt otro likumu
Kirhhofs noteiktai kontūrai, seko
ievērot šādus noteikumus:
-
patvaļīgi
izvēlieties kontūras apiešanas virzienu,
piemēram, pulksteņrādītāja virzienā (18. att.). -
emf
un sprieguma kritumi, kas atbilst
virzienā ar izvēlēto virzienu
apvedceļš ir rakstīti izteiksmē ar
zīme "+"; ja e.f.s. un sprieguma kritums
neatbilst virzienam
kontūru, tad pirms tiem ir zīme
«-».
Piemēram,
18. attēla kontūrai Kirhhofa otrais likums
tiks rakstīts šādi:
U1
– U2
+ U3
=E1
– E3
– E4
(21)
(20) vienādojums var būt
pārrakstīt kā:
(Ui
-Ei)
= 0 (22)
Kur
(U
– E)
- sasprindzinājums uz zara.
Sekojoši,
Var formulēt Kirhofa otro likumu
šādā veidā:
Algebriskā
zaru spriegumu summa jebkurā
slēgtā cilpa ir nulle.
Potenciāls
kalpo iepriekš apspriestā diagramma
otrā grafiskā interpretācija
Kirhhofa likums.
Uzdevums numurs 1.
AT
ķēdei 1. attēlā ir dotas strāvas I1
un es3,
pretestība un emf Noteikt strāvas
es4,
es5,
es6
; spriegums starp punktiem a
un b
ja es1
= 10mA,
es3
= -20 mA,
R4
= 5 kOhm,
E5
= 20 B,
R5
= 3kOhm,
E6
= 40 B,
R6
= 2kOhm.
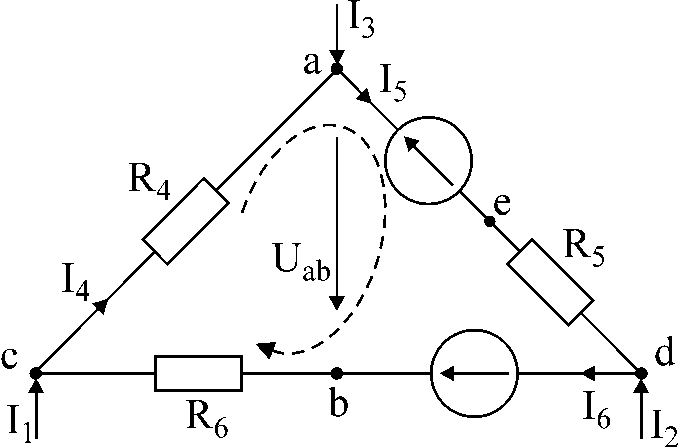
1. att
Risinājums:
-
Par doto
kontūru, mēs sastādām divus vienādojumus saskaņā ar
Kirhhofa pirmais likums un viens - saskaņā ar
otrais. Kontūras virziens
norādīts ar bultiņu.

AT
risinājuma rezultātā iegūstam: I6
= 0; es4
= 10mA;
es5
= -10mA
-
jautāt
sprieguma virziens starp punktiem
a
un b
no punkta "a"
uz punktu "b"
— Uab.
Šo spriegumu var atrast no vienādojuma
Otrais Kirhhofa likums:
es4R4
+ Uab
+ es6R6
= 0
Uab
= - 50 V.
Uzdevums numurs 2.
Priekš
diagrammas 2. attēlā sastāda vienādojumus saskaņā ar
Kirhhofa likumi un nosaka nezināmo
punktus.
Ņemot vērā:
es1
= 20mA;
es2
= 10mA
R1
= 5 kOhm,
R3
= 4 kOhm,
R4
= 6 kOhm,
R5
= 2kOhm,
R6
= 4kΩ.
2. att
Risinājums:
Mezglu skaits
vienādojumi - 3, kontūrvienādojumu skaits
– 1.
Atcerieties!
Sastādot vienādojumu saskaņā ar otro
Kirhhofa likums, mēs izvēlamies kontūru, in
kas neietver pašreizējos avotus.
Kontūras virziens ir norādīts attēlā.
AT
šīs ķēdes zaru strāvas I1
un es2.
Nezināms
straumes
es3,
es4,
es5,
es6.

Lemjot
sistēma, mēs iegūstam: I3
= 13,75 mA;
es4
= -3,75 mA;
es5
= 6,25 mA;
es6
= 16,25 mA.
Pamatjēdzieni
Elektriskā strāva plūst, kad slēgta ķēde ļauj elektroniem ķēdē pārvietoties no augsta potenciāla uz zemāku. Citiem vārdiem sakot, strāvai ir nepieciešams elektronu avots, kam ir enerģija, lai tos iekustinātu, kā arī negatīvo lādiņu atgriešanās punkts, ko raksturo to trūkums. Kā fiziska parādība strāvu ķēdē raksturo trīs pamatlielumi:
- spriegums;
- strāvas stiprums;
- vadītāja pretestība, caur kuru pārvietojas elektroni.
Spēks un spriedze
Strāvas stiprums (I, mērīts ampēros) ir elektronu (lādiņa) tilpums, kas laika vienībā pārvietojas pa vietu ķēdē. Citiem vārdiem sakot, mērījums I ir kustībā esošo elektronu skaita noteikšana
Ir svarīgi saprast, ka šis termins attiecas tikai uz kustību: statiskajiem lādiņiem, piemēram, uz nepievienota akumulatora spailēm, nav izmērāmas vērtības I. Strāvu, kas plūst vienā virzienā, sauc par tiešo (DC), un periodiski mainīgu virzienu sauc par mainīgu (AC). Spriegumu var ilustrēt ar tādu parādību kā spiediens vai kā objektu potenciālās enerģijas atšķirības gravitācijas ietekmē
Lai radītu šo nelīdzsvarotību, vispirms ir jāiztērē enerģija, kas atbilstošos apstākļos tiks realizēta kustībā. Piemēram, krītot slodzei no augstuma, tiek veikti darbi tās pacelšanai, galvaniskajos akumulatoros potenciālā starpība pie spailēm veidojas ķīmiskās enerģijas pārvēršanas dēļ, ģeneratoros - iedarbības rezultātā elektromagnētiskais lauks
Stresu var ilustrēt ar tādu parādību kā spiediens vai kā objektu potenciālās enerģijas atšķirības gravitācijas ietekmē. Lai radītu šo nelīdzsvarotību, vispirms ir jāiztērē enerģija, kas atbilstošos apstākļos tiks realizēta kustībā. Piemēram, krītot slodzei no augstuma, tiek realizēts tās pacelšanas darbs, galvaniskajos akumulatoros potenciālā starpība pie spailēm veidojas ķīmiskās enerģijas pārvēršanas rezultātā, ģeneratoros - iedarbības rezultātā. elektromagnētiskais lauks.
Vadītāja pretestība
Neatkarīgi no tā, cik labs ir parasts vadītājs, tas nekad neļaus elektroniem iziet cauri bez zināmas pretestības to kustībai. Pretestību var uzskatīt par mehāniskās berzes analogu, lai gan šis salīdzinājums nebūs ideāls.Kad strāva plūst caur vadītāju, kāda potenciālu starpība tiek pārvērsta siltumā, tāpēc rezistoram vienmēr būs sprieguma kritums. Elektriskie sildītāji, fēni un citas līdzīgas ierīces ir paredzētas tikai elektroenerģijas izkliedēšanai siltuma veidā.
Vienkāršotā pretestība (apzīmēta kā R) ir mērs, cik lielā mērā ķēdē tiek aizkavēta elektronu plūsma. To mēra omos. Rezistora vai cita elementa vadītspēju nosaka divas īpašības:
- ģeometrija;
- materiāls.
Formai ir ārkārtīgi liela nozīme, kā tas izriet no hidrauliskās analoģijas: izspiest ūdeni pa garu un šauru cauruli ir daudz grūtāk nekā izspiest ūdeni pa īsu un platu. Materiāliem ir izšķiroša loma. Piemēram, elektroni var brīvi pārvietoties vara stieplē, bet nevar plūst caur izolatoriem, piemēram, gumiju, neatkarīgi no to formas. Papildus ģeometrijai un materiālam ir arī citi faktori, kas ietekmē vadītspēju.
Oma likuma interpretācija
Lai nodrošinātu lādiņu kustību, ķēde ir jāaizver. Ja nav papildu jaudas, strāva nevar pastāvēt ilgu laiku. Potenciāls ātri vien kļūs līdzvērtīgs. Lai uzturētu ķēdes darbības režīmu, ir nepieciešams papildu avots (ģenerators, akumulators).
Pilnajā ķēdē būs visu komponentu kopējā elektriskā pretestība. Precīziem aprēķiniem tiek ņemti vērā zudumi vadītājos, pretestības elementos un strāvas avotā.
Cik liels spriegums jāpieliek noteiktai strāvas stiprumam, aprēķina pēc formulas:
U=I*R.
Līdzīgi ar aplūkoto attiecību palīdzību tiek noteikti arī citi ķēdes parametri.
Paralēlais un seriālais savienojums
Elektrikā elementi tiek savienoti vai nu virknē - viens pēc otra vai paralēli - tas ir tad, kad vienam punktam ir pievienotas vairākas ieejas, bet izejas no tiem pašiem elementiem ir savienotas ar citu.
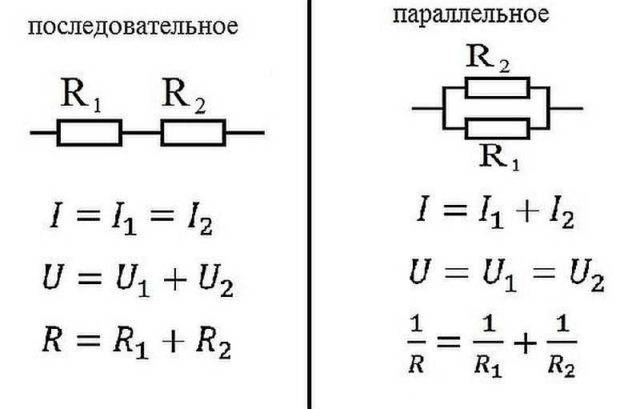
Oma likums paralēlajam un virknes savienojumam
seriālais savienojums
Kā Ohma likums darbojas šajos gadījumos? Savienojot virknē, strāva, kas plūst caur elementu ķēdi, būs vienāda. Spriegums ķēdes posmam ar virknē savienotiem elementiem tiek aprēķināts kā spriegumu summa katrā sekcijā. Kā to var izskaidrot? Strāvas plūsma caur elementu ir lādiņa daļas pārnešana no vienas tā daļas uz otru. Es domāju, tas ir kāds darbs. Šī darba apjoms ir spriedze. Tā ir stresa fiziskā nozīme. Ja tas ir skaidrs, mēs ejam tālāk.
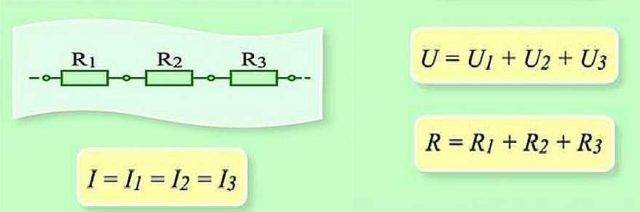
Šīs ķēdes sadaļas seriālais savienojums un parametri
Savienojot virknē, lādiņš pēc kārtas jāpārnes caur katru elementu. Un katram elementam tas ir noteikts darba “apjoms”. Un, lai atrastu darba apjomu visā ķēdes sadaļā, jums jāpievieno darbs pie katra elementa. Tātad izrādās, ka kopējais spriegums ir katra elementa spriegumu summa.
Tādā pašā veidā - ar pievienošanas palīdzību - tiek atrasta arī ķēdes sekcijas kopējā pretestība. Kā jūs to varat iedomāties? Strāva, kas plūst caur elementu ķēdi, secīgi pārvar visas pretestības. Vienu pēc otra. Tas ir, lai atrastu pretestību, kuru viņš pārvarēja, ir jāsaskaita pretestības. Vairāk vai mazāk kā šis. Matemātiskā atvasināšana ir sarežģītāka, un ir vieglāk saprast šī likuma mehānismu.
Paralēlais savienojums
Paralēlais savienojums ir tad, kad vadītāju / elementu sākumi saplūst vienā punktā, bet citā to gali ir savienoti. Mēģināsim izskaidrot likumus, kas ir spēkā šāda veida savienojumiem. Sāksim ar pašreizējo. Elementu savienojuma punktā tiek piegādāta noteikta lieluma strāva. Tas atdalās, plūstot cauri visiem vadītājiem. No tā mēs secinām, ka kopējā strāva sadaļā ir vienāda ar strāvas summu katrā no elementiem: I = I1 + I2 + I3.
Tagad par spriegumu. Ja spriegums ir darbs, lai pārvietotu lādiņu, tad darbs, kas nepieciešams, lai pārvietotu vienu lādiņu, būs vienāds jebkuram elementam. Tas ir, katra paralēli savienotā elementa spriegums būs vienāds. U=U1=U2=U3. Ne tik jautri un vizuāli kā Oma likuma skaidrojuma gadījumā ķēdes posmam, bet saprast var.
Paralēlā savienojuma likumi
Attiecībā uz pretestību lietas ir nedaudz sarežģītākas. Ieviesīsim vadītspējas jēdzienu. Šis ir raksturlielums, kas norāda, cik viegli vai grūti ir lādiņam iziet cauri šim vadītājam. Skaidrs, ka jo mazāka pretestība, jo vieglāk strāvai pāriet. Tāpēc vadītspēja - G - tiek aprēķināta kā pretestības apgrieztā vērtība. Formulā tas izskatās šādi: G = 1/R.
Kāpēc mēs runājam par vadītspēju? Tā kā sekcijas kopējā vadītspēja ar paralēlu elementu savienojumu ir vienāda ar katras sekciju vadītspējas summu. G = G1 + G2 + G3 - viegli saprotams. Tas, cik viegli strāva pārvarēs šo paralēlo elementu mezglu, ir atkarīgs no katra elementa vadītspējas. Tātad izrādās, ka tie ir jāsaloka.
Tagad mēs varam pāriet uz pretestību. Tā kā vadītspēja ir pretestības apgrieztā vērtība, mēs varam iegūt šādu formulu: 1/R = 1/R1 + 1/R2 + 1/R3.
Kas mums nodrošina paralēlo un seriālo savienojumu?
Teorētiskās zināšanas ir labas, bet kā tās pielietot praksē? Jebkāda veida elementus var savienot paralēli un virknē. Bet mēs izskatījām tikai visvienkāršākās formulas, kas apraksta lineāros elementus. Lineārie elementi ir pretestības, ko sauc arī par "rezistoriem". Lūk, kā varat izmantot apgūto:
Ja nav pieejams lielas vērtības rezistoru, bet ir vairāki mazāki, vēlamo pretestību var iegūt, savienojot virknē vairākus rezistorus. Kā redzat, šī ir noderīga tehnika.
Lai pagarinātu bateriju kalpošanas laiku, tās var savienot paralēli. Šajā gadījumā spriegums, saskaņā ar Oma likumu, paliks nemainīgs (par to varat pārliecināties, izmērot spriegumu ar multimetru). Un dubultā akumulatora “darba ilgums” būs daudz ilgāks nekā diviem elementiem, kas nomainīs viens otru
Vienkārši ievērojiet: paralēli var pieslēgt tikai barošanas avotus ar tādu pašu potenciālu. Tas nozīmē, ka nevar savienot mirušu un jaunu akumulatoru.
Ja joprojām izveidojat savienojumu, akumulators, kuram ir lielāks uzlādes līmenis, mēdz uzlādēt mazāk uzlādētu. Tā rezultātā to kopējā maksa samazināsies līdz zemai vērtībai.
Kopumā šie ir visizplatītākie šo savienojumu lietojumi.
Ideāls EMF avots
Elektromotora spēks (E) ir fizikāls lielums, kas nosaka ārējo spēku ietekmes pakāpi uz kustību slēgtā lādiņnesēju ķēdē. Citiem vārdiem sakot, tas, cik spēcīgi strāva mēdz plūst caur vadītāju, būs atkarīgs no EML.
Izskaidrojot šādas nesaprotamas parādības, vietējie skolu skolotāji labprāt pievēršas hidrauliskās analoģijas metodei.Ja vadītājs ir caurule un elektriskā strāva ir caur to plūstošais ūdens daudzums, tad EMF ir spiediens, ko sūknis attīsta, lai sūknētu šķidrumu.
Termins elektromotora spēks ir saistīts ar tādu jēdzienu kā spriegums. Viņa, EMF, tiek mērīta arī voltos (vienība - "V"). Katram enerģijas avotam, neatkarīgi no tā, vai tas ir akumulators, ģenerators vai saules panelis, ir savs elektromotora spēks. Bieži vien šis EMF ir tuvu izejas spriegumam (U), bet vienmēr nedaudz mazāks par to. To izraisa avota iekšējā pretestība, uz kuras daļa sprieguma neizbēgami samazinās.
Šī iemesla dēļ ideāls EML avots drīzāk ir abstrakts jēdziens vai fizisks modelis, kam nav vietas reālajā pasaulē, jo akumulatora Rin iekšējā pretestība, lai arī ļoti zema, tomēr atšķiras no absolūtās nulles.
Ideāls un īsts emf avots
Diferenciālā formā
Formula ļoti bieži tiek pasniegta diferenciālā formā, jo vadītājs parasti ir neviendabīgs, un tas būs jāsadala pēc iespējas mazākās daļās. Caur to ejošā strāva ir saistīta ar lielumu un virzienu, tāpēc to uzskata par skalāru lielumu. Ikreiz, kad ir jāatrod iegūtā strāva caur vadu, tiek ņemta visu atsevišķo strāvu algebriskā summa. Tā kā šis noteikums attiecas tikai uz skalārajiem lielumiem, strāva arī tiek uzskatīta par skalāru lielumu. Ir zināms, ka strāva dI = jdS iet cauri sadaļai. Spriegums uz tā ir vienāds ar Edl, tad vadam ar nemainīgu šķērsgriezumu un vienādu garumu attiecība būs patiesa:
 Diferenciālā forma
Diferenciālā forma
Tāpēc strāvas izteiksme vektora formā būs: j = E.
Svarīgs! Metālvadītāju gadījumā, palielinoties temperatūrai, vadītspēja samazinās, bet pusvadītājiem tā palielinās. Omova likums nepierāda stingru samērīgumu
Lielai metālu un sakausējumu grupai pretestība pazūd absolūtajai nullei tuvu temperatūrā, un šo procesu sauc par supravadītspēju.